SISTEMÁTICA GRACELI - TEORIA  GERAL DOS SISTEMAS.

QUE TANTO É UM RAMO DA MATEMÁTICA PURA, QUANTO NA TOPOLOGIA, GEOMETRIA, TOPOGEOMETRIA GRACELI, E NA FÍSICA.

OS SISTEMAS SE DIVIDEM EM:

 DINÂMICOS.

CONJUGADOS EM RELAÇÕES DE MAIS DE UM , COMO OS SISTEMAS QUÂNTICOS, INTERAÇÕES DE ENERGIAS, CAMPOS FORÇAS, E PARTÍCULAS, E COM O MEIO AMBIENTE, E FENÔMENOS FÍSICOS.

ESTATÍSTICOS QUE REFLETEM RELAÇÕES DE PROPORCIONALIDADE E VARIAÇÕES TEMPORAIS, ESPACIAIS FENÊMENICAS.

COMPLEXOS, COMO EM RELAÇÕES TRANSCENDENTES E QUÂNTICAS E DE DIMENSÕES, RELAÇÕES MATEMÁTICAS EM VARIÁVEIS COMPLEXAS E OUTRAS, TANTO NA BIOLOGIA, E OUTROS.

HARMÔNICOS. RELAÇÕES DE HARMÔNICAS E QUE NÃO REFLETEM OS ALEATÓRIOS. COMO OS ESFÉRICOS HARMÔNICOS NA FÍSICA.

ALEATÓRIOS, E ALEATORISO QUÂNTICOS RELATIVISTAS E INDETERMINADOS, E TRANSCENDENTES , COMO TAMBÉM NA FÍSICA. E MOVIMENTOS DE INTERAÇÕES ALEATÓRIAS.

GEOMÉTRICOS  COMO EM VARIÁVEIS DE ESTRUTURAS E FORMAS GEOMÉTRICAS E TOPOLÓGICAS.

ESTRUTURAIS - QUE REFLETEM AS ESTRUTURAS E SUAS TRANSFORMAÇÕES E INTERAÇÕES COMO PARTÍCULAS, E OUTROS.

FENOMÊMENICOS - COMO NAS INTERAÇÕES QUÂNTICAS E INTERAÇÕES SPINS-ÓRBITAS.

ESTRUTURAS MOLECULARES E DINÂMICAS E SUAS TRANSFORMAÇÕES - COMO NAS ESTRURURAS MOLECULARES, E OUTROS.

HARMÔNICOS ESFÉRICOS.

TRANSFORMATIVOS - COMO EM TROCAS E INTERAÇÕES DE ENERGIAS, ENTROPIAS E ENTALPIAS

CATEGORIAIS E DIMENSIONAIS - COMO AS CATEGORIAS DE GRACELI E SUAS DIMENSÕES.  TENSORES E OPERADORES.

OS FÍSICOS QUIMICOS E BIOLÓGICOS.

OS ASTRONÔMICOS. E OUTROS.

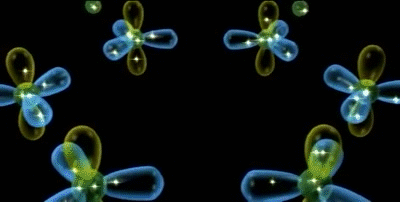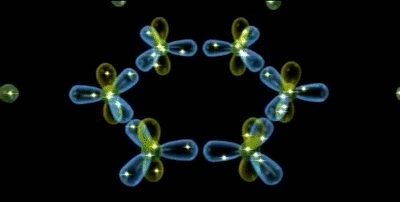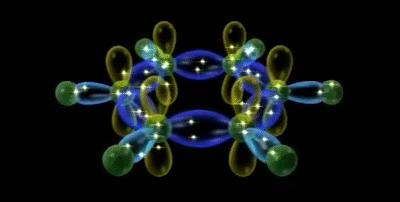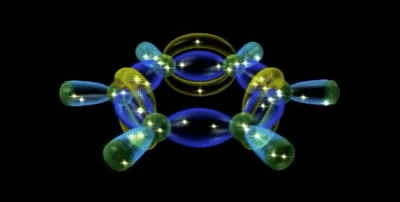
Em matemática e ciência física, harmónicos esféricos são funções harmónicas que representam a variação espacial de um conjunto ortogonal de soluções da equação de Laplace, quando a solução é expressa em coordenadas esféricas.

Os harmónicos esféricos são importantes em muitas aplicações teóricas e práticas, particularmente em física atómica (uma vez que a função de onda do electrão contém harmónicos esféricos) e na teoria do potencial, tanto no campo gravitacional como na eletrostática.

Introdução

Harmónicos esféricos de variável real Ylm, para l =0,...,4 (de cima para baixo) e m = 0,...,4 (da esquerda para a direita). Os harmónicos Yl-m com m negativo são idênticos, mas com uma rotação de 90º/m em torno do eixo z em relação aos harmónicos positivos.

A equação de Laplace em coordenadas esféricas é dada por:

(Ver também Nabla e laplaciano em coordenadas esféricas). Se nesta expressão considera-se soluções específicas da forma , a parte angular Y é chamada harmónico esférico e satisfaz a relação

Se, por sua vez, utiliza-se o método de separação de variáveis para esta equação, pode-se ver que a equação acima admite soluções periódicas nas duas coordenadas angulares (l é um inteiro). Logo, a solução periódica do sistema anterior depende de dois inteiros (l, m) e é dada em termos de funções trigonométricas e dos polinômios associados de Legendre:

Onde:  é chamada de função harmónica esférica de grau  e ordem ;  é o polinómio associado de Legendre;  é uma constante de normalização; e  e  representam os parâmetros angulares (respectivamente, o ângulo azimutal ou colatitude e o ângulo polar ou longitude).

As coordenadas esféricas utilizadas neste artigo são consistentes com àquelas usadas pelos físicos, mas diferem das utilizadas pelos matemáticos (ver coordenadas esféricas). Em particular, a colatitude , ou ângulo polar, assume valores de  e a longitude , ou azimute, está na faixa de . Portanto,  é nulo no Pólo Norte,  no Equador e  no Pólo Sul.

Quando a equação de Laplace é resolvida em coordenadas esféricas, as condições de periodicidade na fronteira da coordenada  e as condições de regularidades nos "Pólos Norte e sul" da esfera condizem com o que foi dito que os números l e m necessários devem ser inteiros que satisfazem  e .

Em matemática e ciência física, harmónicos esféricos são funções harmónicas que representam a variação espacial de um conjunto ortogonal de soluções da equação de Laplace, quando a solução é expressa em coordenadas esféricas.

Os harmónicos esféricos são importantes em muitas aplicações teóricas e práticas, particularmente em física atómica (uma vez que a função de onda do electrão contém harmónicos esféricos) e na teoria do potencial, tanto no campo gravitacional como na eletrostática.

Introdução

Harmónicos esféricos de variável real Y_lm, para l =0,...,4 (de cima para baixo) e m = 0,...,4 (da esquerda para a direita). Os harmónicos Y_l-m com m negativo são idênticos, mas com uma rotação de 90º/m em torno do eixo z em relação aos harmónicos positivos.

A equação de Laplace em coordenadas esféricas é dada por:

${\displaystyle \nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0}$

(Ver também Nabla e laplaciano em coordenadas esféricas). Se nesta expressão considera-se soluções específicas da forma ${\displaystyle f(r,\theta ,\phi )=R(r)Y(\theta ,\varphi )}$, a parte angular Y é chamada harmónico esférico e satisfaz a relação

${\displaystyle {1 \over \sin \theta }{d \over d\theta }\left(\sin \theta {dY(\theta ,\varphi ) \over d\theta }\right)+{1 \over \sin ^{2}\theta }{d^{2}Y(\theta ,\varphi ) \over d\varphi ^{2}}+l(l+1)Y(\theta ,\varphi )=0}$

Se, por sua vez, utiliza-se o método de separação de variáveis para esta equação, pode-se ver que a equação acima admite soluções periódicas nas duas coordenadas angulares (l é um inteiro). Logo, a solução periódica do sistema anterior depende de dois inteiros (l, m) e é dada em termos de funções trigonométricas e dos polinômios associados de Legendre:

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=N\,e^{im\varphi }\,P_{\ell }^{m}(\cos {\theta })}$

Onde: ${\displaystyle Y_{\ell }^{m}}$ é chamada de função harmónica esférica de grau ${\displaystyle \ell }$ e ordem ${\displaystyle m}$; ${\displaystyle P_{\ell }^{m}}$ é o polinómio associado de Legendre; ${\displaystyle N}$ é uma constante de normalização; e ${\displaystyle \theta }$ e ${\displaystyle \varphi }$ representam os parâmetros angulares (respectivamente, o ângulo azimutal ou colatitude e o ângulo polar ou longitude).

As coordenadas esféricas utilizadas neste artigo são consistentes com àquelas usadas pelos físicos, mas diferem das utilizadas pelos matemáticos (ver coordenadas esféricas). Em particular, a colatitude ${\displaystyle \theta }$, ou ângulo polar, assume valores de ${\displaystyle 0\leq \theta \leq \pi }$ e a longitude ${\displaystyle \varphi }$, ou azimute, está na faixa de ${\displaystyle 0\leq \varphi <2\pi }$. Portanto, ${\displaystyle \theta }$ é nulo no Pólo Norte, ${\displaystyle \pi /2}$ no Equador e ${\displaystyle \pi }$ no Pólo Sul.

Quando a equação de Laplace é resolvida em coordenadas esféricas, as condições de periodicidade na fronteira da coordenada ${\displaystyle \varphi }$ e as condições de regularidades nos "Pólos Norte e sul" da esfera condizem com o que foi dito que os números l e m necessários devem ser inteiros que satisfazem ${\displaystyle \ell \geq 0}$ e ${\displaystyle |m|\leq \ell }$.

Normalização

Há várias normalizações utilizadas para as funções harmónicas esféricas. Em física e sismologia essas funções são geralmente definidas como

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=A_{\ell }^{m}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

onde

${\displaystyle A_{\ell }^{m}={\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}}$

Estas funções são ortonormalizadas,

${\displaystyle \int _{\varphi =0}^{2\pi }d\varphi \int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$,

onde δ_aa = 1, δ_ab = 0 se a ≠ b (ver delta de Kronecker). Nas áreas de geodésia e análise espectral utiliza-se

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1)}{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

que possui um termo linear

${\displaystyle {1 \over 4\pi }\int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$.

No magnetismo, no entanto, usa-se os harmónicos de Schmidt semi-normalizados,

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {(\ell -m)! \over (\ell +m)!}}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

que possuem a seguinte normalização:

${\displaystyle \int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,={4\pi \over (2\ell +1)}\delta _{\ell \ell '}\,\delta _{mm'}}$.

Utilizando a identidade (ver funções associadas de Legendre)

${\displaystyle P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}}$

pode-se demonstrar que todas as funções harmónicas esféricas normalizadas acima satisfazem

${\displaystyle Y_{\ell }^{m*}(\theta ,\varphi )=(-1)^{m}Y_{\ell }^{-m}(\theta ,\varphi )}$,

onde o símbolo * significa conjugação complexa.

Convenção de fase de Condon-Shortley

Um forte motivo para uma confusão com a definição de harmónicos esféricos é o fator de fase ${\displaystyle (-1)^{m}\,}$, normalmente identificado como a fase de Condon-Shortley na literatura quântica. Na mecânica quântica, é uma prática usual incluir este fator de fase na definição das funções associadas de Legendre, ou anexá-lo à definição de funções harmónicas esféricas. Não há nenhuma exigência da utilização da fase de Condon-Shortley na definição de funções harmónicas esféricas, mas se ela for incluída, então algumas operações no domínio da mecânica quântica serão mais simples. No magnetismo e na geodésia, ao contrário, nunca incluiu-se o fator de fase Condon-Shortley na definição dos harmónicos esféricos.

Expansão em harmónicos esféricos

Os harmónicos esféricos formam um conjunto completo ortonormal de funções e, portanto, formam um espaço vetorial análogo aos vetores unitários da base. Na esfera unitária, todas as funções de quadrado integrável podem, portanto, ser expandidas como uma combinação linear de:

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{m}\,Y_{\ell }^{m}(\theta ,\varphi )}$.

Essa expansão é exata sempre que ${\displaystyle \ell }$ estende-se até o infinito. Haverá um erro de truncamento ao limitar a soma sobre ${\displaystyle \ell }$ numa largura de banda finita ${\displaystyle L}$. Os coeficientes da expansão ${\displaystyle f_{\ell }^{m}}$ podem ser obtidos multiplicando-se a equação pelo conjugado complexo dos harmónicos esféricos, integrando-se sobre um ângulo sólido ${\displaystyle \Omega \!\,}$ e usando-se as relações de ortogonalidade acima. No caso de harmónicos ortonormalizados, obtemos

${\displaystyle f_{\ell }^{m}=\int _{\Omega }f(\theta ,\varphi )\,Y_{\ell }^{m*}(\theta ,\varphi )d\Omega =\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \sin \theta f(\theta ,\varphi )Y_{\ell }^{m*}(\theta ,\varphi )}$.

Um conjunto alternativo de harmónicos esféricos para funções reais pode ser obtido a partir do conjunto

${\displaystyle Y_{\ell m}={\begin{cases}Y_{\ell }^{0}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad {\mbox{ si }}m=0\\{1 \over {\sqrt {2}}}\left(Y_{\ell }^{m}+(-1)^{m}\,Y_{\ell }^{-m}\right)={\sqrt {2}}NP_{\ell }^{m}(\theta )\cos m\varphi \qquad \quad \quad {\mbox{si }}m>0\\{1 \over i{\sqrt {2}}}\left(Y_{\ell }^{|m|}-(-1)^{|m|}\,Y_{\ell }^{-|m|}\right)={\sqrt {2}}NP_{\ell }^{|m|}(\theta )\sin |m|\varphi \quad {\mbox{ si }}m<0.\end{cases}}}$

Estas funções têm as mesmas propriedades que as funções de normalização complexas dadas anteriormente. Nesta forma, uma função real integrável pode ser expressa como uma soma infinita de harmónicos esféricos

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{lm}\,Y_{lm}(\theta ,\varphi )}$.

Harmónicos esféricos em física

Seguem-se algumas aplicações dos harmónicos esféricos na física, tanto na eletrostática como na mecânica quântica.

Harmónicos esféricos na eletrostática

O átomo de hidrogênio

Ver artigo principal: Átomo de Hidrogênio

O modelo quântico moderno do átomo de hidrogênio assume o elétron em um estado constante de energia tem sua posição distribuída ao redor do núcleo atômico como uma distribuição de probabilidades, cuja variação angular é dada por um harmónico esférico.

Análise espectral

A potência total de uma função ${\displaystyle f}$ é definida na linguagem de processamento de sinais eletrônicos como sendo a integral do quadrado da função dividida pela área varrida por ela. Usando as propriedades de ortonormalização de funções harmónicas esféricas de potência real unitária, é fácil verificar que a potência total de uma função definida na esfera unitária está relacionada aos seus coeficientes espectrais através de uma generalização do teorema de Parseval:

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )^{2}\,d\Omega =\sum _{l=0}^{\infty }S_{f\!f}(l)}$,

onde

${\displaystyle S_{f\!f}(l)=\sum _{m=-l}^{l}f_{lm}^{2}}$

é definido como o espectro de potência angular. Da mesma forma, pode-se definir a potência cruzada entre duas funções como

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )\,g(\Omega )\,d\Omega =\sum _{l=0}^{\infty }S_{fg}(l)}$,

onde

${\displaystyle S_{fg}(l)=\sum _{m=-l}^{l}f_{lm}g_{lm}}$

é definido como o espectro cruzado neste caso. Se as funções ${\displaystyle f}$ e ${\displaystyle g}$ possuem valor médio igual a zero (ou seja, com coeficientes espectrais ${\displaystyle f_{00}}$ e ${\displaystyle g_{00}}$ nulos), então ${\displaystyle S_{f\!f}(l)}$ e ${\displaystyle S_{fg}(l)}$ representam as contribuições para a variância e covariância da função para ${\displaystyle \ell }$, respectivamente. É comum que o espectro de potência cruzado seja aproximado por uma lei de potências do tipo

${\displaystyle S_{f\!f}(l)=C\,\ell ^{\beta }}$.

Quando ${\displaystyle \beta =0}$, o espectro é "branco", pois cada nível tem potências iguais. Quando ${\displaystyle \beta <0}$, o espectro é chamado de "vermelho", porque não há mais energia nos níveis mais baixos com comprimentos de onda mais longos do que nos níveis mais elevados. Finalmente, quando ${\displaystyle \beta >0}$, o espectro é chamado de "azul".

Teorema da adição

Um resultado matemático de grande interesse e utilidade é chamado teorema da adição para harmónicos esféricos. Se dois vetores r e r' tem coordenadas esféricas ${\displaystyle (r,\theta ,\varphi )}$ e ${\displaystyle (r',\theta ',\varphi ')}$, respectivamente, o ângulo ${\displaystyle \gamma }$ entre eles é dado pela expressão

${\displaystyle \cos \gamma =\cos \theta \cos \theta '+\sin \theta \sin \theta '\cos(\varphi -\varphi ')}$.

O teorema da adição expressa um polinômio de Legendre de ordem ${\displaystyle l}$ no ângulo ${\displaystyle \gamma }$ em termos de produtos de dois harmónicos esféricos com coordenadas angulares ${\displaystyle (\theta ,\varphi )}$ e ${\displaystyle (\theta ',\varphi ')}$:

${\displaystyle P_{l}(\cos \gamma )={\frac {4\pi }{2l+1}}\sum _{m=-l}^{l}Y_{lm}^{*}(\theta ',\phi ')\,Y_{lm}(\theta ,\varphi )}$.

Esta expressão é válida tanto para harmónicos reais como complexos. Entretanto, deve-se ressaltar que a fórmula apresentada anteriormente é válida apenas para harmónicos esféricos ortonormalizados. Harmónicos de potência unitária são necessários para eliminar o fator ${\displaystyle 4\pi }$ da expressão anterior.

Visualizando os harmónicos esféricos

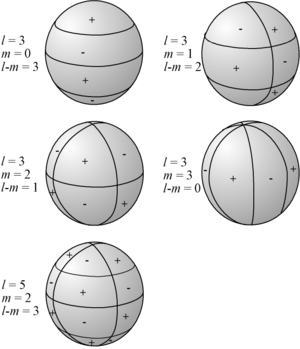
Representação esquemática de Y_lm sobre a esfera unitária. Y_lm é igual a 0 ao longo de m círculos que passam pelos polos e ao longo de l-m círculos de mesma latitude. A função muda de sinal cada vez que cruza uma dessas linhas.

A função harmónica esférica real Y₃₂ mostrada ao longo de quatro cortes.

Os harmónicos esféricos são facilmente visualizados através da contagem do número de cruzamentos que ambos estão na direção das coordenadas ${\displaystyle \theta }$ e ${\displaystyle \varphi }$. Para obter a orientação sobre ${\displaystyle \theta }$, as funções associadas de Legendre possuem ${\displaystyle l-|m|}$ zeros, enquanto que na coordenada ${\displaystyle \varphi }$ as funções trigonométricas seno e cosseno possuem ${\displaystyle 2|m|}$ zeros.

Quando o harmónico esférico de ordem ${\displaystyle m}$ é nulo, as funções harmónicas esféricas não dependem de ${\displaystyle \varphi }$, e diz-se que a função é zonal. Quando ${\displaystyle l=|m|}$, não existem zeros na direção ${\displaystyle \theta }$, e diz-se que a função é setorial. Nos outros casos, as funções formam um padrão em xadrez sobre a esfera.

Expressões analíticas para os primeiros harmónicos esféricos

Eis as expressões analíticas dos primeiros harmónicos esféricos ortonormalizados, com a convenção de fase de Condon-Shortley:

${\displaystyle Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}}$

${\displaystyle Y_{1}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{-i\varphi }}$

${\displaystyle Y_{1}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over \pi }}\,\cos \theta }$

${\displaystyle Y_{1}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{-2i\varphi }}$

${\displaystyle Y_{2}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{-i\varphi }}$

${\displaystyle Y_{2}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {5 \over \pi }}\,(3\cos ^{2}\theta -1)}$

${\displaystyle Y_{2}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{2i\varphi }}$

${\displaystyle Y_{3}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {7 \over \pi }}\,(5\cos ^{3}\theta -3\cos \theta )}$

Ver também: [[:[[Tabela de harmónicos esféricos até Y₁₀]]]]

Em mecânica (especialmente em mecânica quântica) e geometria, o grupo de rotação ou SO(3) é o grupo de todas as rotações sobre a origem de um espaço euclidiano tridimensional R³ sob a operação de composição.

Por definição, uma rotação sobre a origem é uma transformação linear que preserva o comprimento dos vetores e preserva a orientação (i.e. o sentido) do espaço. Uma transformação preservante de comprimento a qual preserva a orientação é chamada uma rotação imprópria.

Compondo duas rotações resulta em outra rotação; cada rotação tem uma única rotação inversa; e a função identidade satisfaz à definição de uma rotação. Apropriando-se das propriedades acima, o conjunto de todas as rotações é um grupo sob composição. Além disso, o grupo de rotação tem uma estrutura de variedade natural para a qual as operações de grupo são suaves; então ele é de fato um grupo de Lie.

Topologia

O grupo SO(3) é simplesmente conectado. Ele pode ser visualizado como uma esfera em ${\displaystyle R^{3}}$ de raio ${\displaystyle \pi }$. O vetor formado por cada ponto nesse volume indica o eixo de rotação. E o seu comprimento, o ângulo de rotação. Pontos antípodas na superfície da esfera representam a mesma rotação.^{[carece de fontes]}

Elementos do grupo

Os elementos do grupo SO(3) são matrizes ortogonais R de dimensão 3 e, portanto, obedecem à relação:

${\displaystyle {\tilde {R}}R=R{\tilde {R}}=1}$

Temos também que ${\displaystyle det(R)=+1}$, sendo portanto um caso especial do grupo O(3) onde ${\displaystyle det(R)=\pm 1}$.

Uma rotação qualquer será simbolizada por um matriz de rotação (letra latina maiúscula), função de um vetor (letra grega), cuja direção será o eixo de rotação e cujo comprimento, o ângulo de rotação.

Exemplo:

${\displaystyle R({\vec {\alpha }})}$

O produto de duas rotações é uma nova rotação pertencente ao grupo.

${\displaystyle R({\vec {\alpha }})R({\vec {\beta }})=R({\vec {\gamma }})}$,

onde

${\displaystyle {\vec {\gamma }}=\gamma ({\vec {\alpha }},{\vec {\beta }})}$.

Álgebra de Lie

A álgebra de Lie do grupo SO(3) é simbolizada como so(3). Ela representa o comportamento local (i.e. rotações infinitesimais) do grupo. A relação entre três elementos do grupo neste caso envolve uma operação chamada de Colchete de Lie.

Geradores

Os vetores que compõem o espaço vetorial desta álgebra são conhecidos como geradores do grupo, sendo assim definidos:

${\displaystyle (L_{i})_{jk}=-i\epsilon _{ijk}}$

Como SO(3) é um grupo compacto, seus elementos podem ser gerados através da expressão

${\displaystyle R(\alpha )=exp(i\sum _{k}\alpha _{k}L_{k}).}$

Em outras palavras, compondo diversas rotações infinitesimais, podemos obter qualquer rotação finita através da expressão acima.

Colchete de Lie

É representado pelos seguintes comutadores:

${\displaystyle [L_{i},L_{j}]=c_{ij}^{k}L_{k}}$,

os quais também podem ser representados por

${\displaystyle [L_{i},L_{j}]=i\epsilon _{ijk}L_{k}}$.

Eles qualificam o fato de que a ordem em que são efetuadas rotações sucessivas é importante para o resultado final obtido.

Estrutura multiplicativa

Definindo-se as constantes ${\displaystyle c_{ij}^{k}}$ (conhecidas como constantes estruturais do grupo) desta forma:

${\displaystyle c_{ij}^{k}=i\epsilon _{ijk},}$

onde ${\displaystyle \epsilon _{ijk}}$ é o tensor ${\displaystyle \epsilon }$ ou símbolo de Levi-Civita.

Podemos então calcular a relação entre os ângulos:

${\displaystyle \gamma _{k}=\alpha _{k}+\beta _{k}+{\frac {i}{2}}c_{mn}^{k}\alpha _{m}\beta _{n}+...}$

Este resultado indica que as constantes estruturais de fato definem o grupo.

Representações

Se tivermos matrizes ${\displaystyle A_{k}}$ que obedeçam à algebra de Lie do grupo, podemos através de exponenciação gerar um conjunto de matrizes D(R) possuindo um comportamento similar ao do grupo original. Este conjunto D(R) é conhecido como uma representação do grupo.

${\displaystyle D(R(\alpha ))=exp(i\sum _{k}\alpha _{k}A_{k}).}$

Mais formalmente, uma representação é um mapeamento entre os elementos do grupo (a pertencente a G) e um certo conjunto de operadores lineares (D(a)) obedecendo à relação

D(a.b) = D(a)D(b).

Na mecânica quântica, a necessidade de se encontrar novas representações deriva do fato de que a função de onda é normalmente composta de uma combinação linear de autofunções de um operador. Após uma operação de rotação, a função pode se transformar como uma nova combinação linear das mesmas autofunções (ou autoestados).

Outra forma de entender o significado das representações é a seguinte:^[1]

Dada uma operação de rotação R, caracterizada por uma matriz ortogonal R, nós associamos um operador D(R) no espaço de ket apropriado tal que

${\displaystyle |\alpha >_{R}=D(R)|\alpha >,}$

onde ${\displaystyle |\alpha >_{R}}$ e ${\displaystyle |\alpha >}$ significam os kets do sistema rotacionado e original, respectivamente. Note que a matriz 3x3 ortogonal R age sobre sobre uma matriz coluna constituída de três componentes de um vetor clássico, enquanto que o operador D(R) age sobre vetores de estados no espaço de kets. A forma matricial de D(R) depende da dimensionalidade N do espaço de kets particular em questão.

Identidade de Jacobi

Naturalmente, os comutadores da álgebra de Lie de SO(3) obedecem à seguinte relação

${\displaystyle [[A,B],C]+[[B,C],A]+[[C,A],B]=0}$

conhecida como Identidade de Jacobi.

Esta relação pode ser estendida às constantes estruturais do grupo.

${\displaystyle c_{ij}^{m}c_{mk}^{n}+c_{jk}^{m}c_{mi}^{n}+c_{ki}^{m}c_{mj}^{n}=0}$

Representação adjunta

Vamos definir n n x n matrizes de acordo com a fórmula

${\displaystyle (C_{i})_{j}^{~}k\equiv -c_{ij}^{k}}$

como as constantes estruturais obedecem à Identidade de Jacobi, então pode-se provar que as matrizes ${\displaystyle C_{i}}$ refletem as relações de comutação do grupo.

${\displaystyle C_{i}C_{j}-C_{j}C_{i}=c_{ij}^{k}C_{k}}$

Através de exponenciação, podemos gerar uma representação do grupo conhecida como representação adjunta. Ela é a representação natural do grupo em sua própria álgebra de Lie.

No caso de SO-3, esta representação coincide com o próprio grupo original, sendo uma exceção à regra.

Representação equivalente

Vamos supor que U é um operador que rearranja os componentes de uma função de onda ${\displaystyle \psi }$.

${\displaystyle {\hat {\psi }}=U\psi }$

Podemos obter uma representação ligeiramente diferente a partir de uma representação existente D através da operação de similaridade

${\displaystyle {\hat {D}}=UDU^{-1}}$

Esta nova representação é conhecida como uma representação equivalente. Sua importância advém do fato de que qualquer representação pode ser tornada unitária através do 'sanduíche' acima (na mecânica quântica, os operadores são unitários para que haja conservação de probabilidade).

Representação irredutível

É uma representação que permanece invariante sob as rotações do grupo. As representações expressas pelos símbolos ${\displaystyle \epsilon _{ijk}}$ e ${\displaystyle \delta _{i}^{j}}$ (delta de Kronecker), interpretados como tensores, são exemplos de representações irredutíveis especiais. Observe que ${\displaystyle \delta _{ij}}$ e ${\displaystyle \delta ^{ij}}$ não são invariantes.

A essência do uso da teoria dos grupos está na identificação destas representações irredutíveis, já que representações em geral são representadas como a soma direta de representações irredutíveis. Elas revelam as simetrias sob as rotações.

Composição de funções de onda

Até agora consideramos uma representação do grupo definida pela rotação do vetor tridimensional ${\displaystyle {\vec {x}}=(x_{1},x_{2},x_{3})}$. Vamos analisar a seguir como construir representações maiores.

Composição numa mesma partícula

Considere dois vetores ${\displaystyle {\vec {x}}=(x_{1},x_{2},x_{3})}$ and ${\displaystyle {\vec {y}}=(y_{1},y_{2},y_{3})}$ transformando sob rotações. Juntos eles formam um vetor de seis dimensões ${\displaystyle {\vec {z}}=(x_{1},x_{2},x_{3},y_{1},y_{2},y_{3})}$ que se transforma como

${\displaystyle {\vec {(}}z)\rightarrow {\vec {(}}z)'=D{\vec {(}}z)}$,

onde a matriz D pode ser decomposta em matrizes 3 x 3 da seguinte maneira:

${\displaystyle D=\left({\begin{array}{cc}R&0\\0&R\end{array}}\right)}$

Esta é uma representação chamada de redutível, que pode ser considerada como a soma direta de duas representações tridimensionais, ou seja

${\displaystyle 6=3\oplus 3}$

Composição em múltiplas partículas

Considere um sistema composto de duas partículas livres com funções de onda ${\displaystyle \psi _{1}({\vec {x}})}$ e ${\displaystyle \psi _{2}({\vec {y}})}$, onde ${\displaystyle {\vec {x}}}$ e ${\displaystyle {\vec {y}}}$ são as coordenadas das partículas. A função de onda ${\displaystyle \Psi }$ do sistema combinado consiste em todos os produtos possíveis das duas funções de onda. Ou seja o produto tensorial, que é denotado por

${\displaystyle \Psi =\psi _{1}\otimes \psi _{2}}$

Sejam ${\displaystyle T_{ij}}$ todos os produtos transformando sob as rotações como

${\displaystyle T_{ij}'\rightarrow T_{ij}'=R_{ii'}R_{jj'}T_{i'j'}}$

É possível decompor este produto em uma soma de termos irredutíveis, simplificando as equações.

Momento angular

Na mecânica quântica (MQ), a teoria do momento angular pode ser totalmente deduzida a partir dos comutadores de so(3). O primeiro passo nesse sentido é determinar todas as representações irredutíveis de dimensão par do grupo SO(3).

Definições

Os operadores observáveis em MQ são representados por matrizes hermitianas. Sejam as matrizes hermitianas ${\displaystyle I_{k}}$, então

${\displaystyle I_{k}^{\dagger }=I_{k}}$.

Suponhamos que estas matrizes comutem de acordo com as regras do grupo, ou seja

${\displaystyle [I_{i},I_{j}]=i\epsilon _{ijk}I_{k}}$.

Vamos definir o operador degrau como

${\displaystyle I_{\pm }=I_{1}\pm iI_{2}}$.

Operador Casimir

O operador Casimir é um operador construído para comutar com todos os geradores da representação. Neste caso, ele é definido como

${\displaystyle I^{2}=I_{1}^{2}+I_{2}^{2}+I_{3}^{2}}$.

Resultados

Após diversas manipulações, chegamos às expressões:^[2]

${\displaystyle I^{2}|l,m>=l(l+1)|l,m>}$.

${\displaystyle I_{3}|l,m>=m|l,m>}$.

${\displaystyle I_{\pm }|l,m>={\sqrt {l(l+1)-m(m\pm 1)}}|l,m\pm 1>}$,

onde ${\displaystyle m=-l,-l+1,-l+2,...,l-2,l-1,l}$. Ou ambos ${\displaystyle l}$ e ${\displaystyle m}$ são inteiros, ou ambos são inteiros mais ${\displaystyle {\frac {1}{2}}}$.

Este é um resultado muito importante. Ele mostra que este tipo de representação depende de um parâmetro ${\displaystyle l}$, de valor múltiplo de 1/2, agindo em um espaço constituído de ${\displaystyle 2l+1}$ estados ${\displaystyle |l,m>}$. No grupo SU(2) estas fórmulas serão usadas para representar os momentos angulares quânticos orbital e intrínseco (spin).

Na teoria das equações diferenciais ordinárias, chama-se de equaçao de Sturm-Liouville, nome dado em homenagem aos matemáticos Jacques Charles François Sturm (1803-1855) e Joseph Liouville (1809-1882), uma equação diferencial real de segunda ordem da forma:

${\displaystyle -{\frac {d}{dx}}\left[p(x){\frac {dy}{dx}}\right]+q(x)y=\lambda w(x)y,\qquad (1).}$

As funções ${\displaystyle p(x)}$, ${\displaystyle q(x)}$, e ${\displaystyle w(x)}$ são parâmetros e, no caso dito regular, são contínuas no intervalo fechado limitado ${\displaystyle [a,b]}$. O problema é normalmente complementado com condições de contorno especificadas. A função ${\displaystyle w(x)}$ é costumeiramente chamada de função "peso" ou função "densidade".

O valor de ${\displaystyle \lambda }$ pode não ser especificado na equação. Encontrar os valores de ${\displaystyle \lambda }$ para os quais existe uma solução não trivial de (1) satisfazendo as condições de contorno constitui o problema de Sturm-Liouville. Tais ${\displaystyle \lambda }$ são chamados de valores próprios ou autovalores.

Utilizando coordenadas polares na equação do fluxo de velocidade de Madelung, obtemos uma equação de Sturm-Liouville^[1]. Aplicando condições adequadas, alguns problemas clássicos da Mecânica Quântica podem ser resolvidos.